|
Emotion
Section revised and extended October,
2000.
In affect control theory, emotion is a transitory affective condition that
registers how an event makes one seem as compared to how one is supposed to be.
A person invokes an emotion that combines with his or her situational identity
and generates a transient impression equivalent to the transient impression
created by the current event. Thereby the person viscerally experiences how the
impact of the event relates to his or her identity. This conception can be
represented schematically as follows.
 (59) (59)
The historically-anchored state is the fundamental EPA profile r'
= [ e e  p p  a]
for the role identity that has been selected for the self in the situation. The
event-generated state is the EPA profile, q' =
[ a]
for the role identity that has been selected for the self in the situation. The
event-generated state is the EPA profile, q' =
[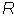 e e 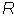 p p
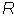 a], for the transient
impression of self produced by the event. The fundamental EPA profile of the
emotion that is appropriate for the person after the event is e' = [ a], for the transient
impression of self produced by the event. The fundamental EPA profile of the
emotion that is appropriate for the person after the event is e' = [ e e  p p  a].
Then the schematic becomes a].
Then the schematic becomes
 (60)
(60)
This shows that emotion can be predicted from the
fundamental profile for self and the transient profile for the post-event self.
The function that relates the three profiles is obtained empirically by
predicting the profile, q, for an emotion
identity combination (like "angry father") from the profile for the
self role identity, r, and the profile for the emotion, e (Heise
and Thomas, 1989):
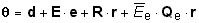 (61)
(61)
or, alternatively,
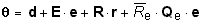 (62)
(62)
where d is a three-element vector of equation constants; E is a
3x3 matrix of coefficients for the emotion profile; R is a 3x3 matrix of
coefficients for the self identity. Qe is a 3x3 matrix of
zeros except for row 1, column 1 which contains a coefficient for the
empirically-discovered interaction term multiplying emotion evaluation times
identity evaluation: EeRe. The interaction
can be represented in either of the ways shown, as needs require.
More generally, nine interactions might be involved in the formation of a
combination impression:  e e e, e,
 p p e, e,
 a a e, e,
 e e p, p,
 p p p, p,
 a a p, p,
 e e a, a, p p a, a,
 a a a.
These can be incorporated into the second matrix equation above for predicting
outcomes tau as follows. Construct a 3x3 diagonal matrix, IRe,
that has the role evaluation a.
These can be incorporated into the second matrix equation above for predicting
outcomes tau as follows. Construct a 3x3 diagonal matrix, IRe,
that has the role evaluation  e
in each diagonal cell and zeros elsewhere; construct a similar matrix, IRp,
with e
in each diagonal cell and zeros elsewhere; construct a similar matrix, IRp,
with  p in the
diagonal entries; and a third diagonal matrix, IRa, with p in the
diagonal entries; and a third diagonal matrix, IRa, with  a
in the diagonal entries. Construct a 3x3 matrix, Qe, that
gives the coefficients for predicting E, P, and A outcomes from the interaction
terms a
in the diagonal entries. Construct a 3x3 matrix, Qe, that
gives the coefficients for predicting E, P, and A outcomes from the interaction
terms  e e e, e,
 p p e,
and e,
and  a a e.
Construct a matrix, Qp, that gives the coefficients for
predicting E, P, and A outcomes from the interaction terms e.
Construct a matrix, Qp, that gives the coefficients for
predicting E, P, and A outcomes from the interaction terms  e e p, p,
 p p p,
and p,
and  a a p.
And construct a matrix, Qa, that gives the coefficients for
predicting E, P, and A outcomes from the interaction terms p.
And construct a matrix, Qa, that gives the coefficients for
predicting E, P, and A outcomes from the interaction terms  e e a, a,
 p p a,
and a,
and  a a a.
Now the prediction equation can be represented as follows. a.
Now the prediction equation can be represented as follows.
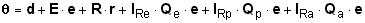 (62a)
(62a)
or
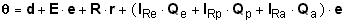 (62b)
(62b)
The alternative form comparable to equation (62b) is
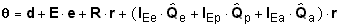 (62c)
(62c)
where the hatted Q matricies represent the same
coefficients as in equation (62b) in a different arrangement.
Solving equation (62b) for e defines emotion in terms of the
fundamental self identity and the transient impression of self.
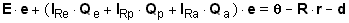 (62c)
(62c)
or
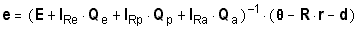 (63)
(63)
This shows that emotion is associated directly with q,
so emotions directly correspond to how events have affected
the self - an interpretation that corresponds to intuitions (e.g., events that
make one look bad also make one feel bad). However, situational identities also
influence emotions in several ways.
People conduct themselves so as to keep transient
impressions of themselves close to their identities, according to the basic
axiom of affect control theory. Therefore the fundamental self role profile, r,
can determine emotion by determining what transient impressions generally arise
as an individual creates events in a situation.
Additionally, the fundamental self profile influences the way that transient
impressions of self translate into emotions. According to equation (63) the
transient self is compared to the fundamental self: this is reflected in
the sub-expression (q - Rr). This
suggests, for example, that people experience especially good
or potent or lively emotions when events make them seem more good or potent or
lively than their identity warrants.
Equation (63) further shows that one's situational role identity influences
the extent to which transient impressions of self translate into more extreme
emotions, because the profile for the role is involved in the matrix inverse
that acts as an overall multiplier in equation (63). The impact of this effect
was examined by analyzing the determinant of matrix [E+  eQe]
for equation 62, using empirical estimates of the coefficients in E and Qe
from the Heise and Thomas (1989) data. eQe]
for equation 62, using empirical estimates of the coefficients in E and Qe
from the Heise and Thomas (1989) data.
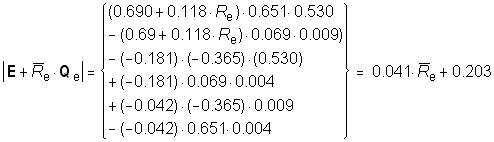 (64)
(64)
When  e = -4.951
the determinant is zero, and the solution is undefined. This cannot happen since
-4.951 is beyond the empirical range of identity evaluations (the measuring
scale goes only to -4.300). However, as self evaluations get very negative the
determinant gets close to zero, the values in the overall matrix multiplier
become very large, and translations of transient self impressions to emotions
are greatly magnified. The implication is that people who
adopt extremely negative identities may experience chaotic emotions, or
emotional lability. e = -4.951
the determinant is zero, and the solution is undefined. This cannot happen since
-4.951 is beyond the empirical range of identity evaluations (the measuring
scale goes only to -4.300). However, as self evaluations get very negative the
determinant gets close to zero, the values in the overall matrix multiplier
become very large, and translations of transient self impressions to emotions
are greatly magnified. The implication is that people who
adopt extremely negative identities may experience chaotic emotions, or
emotional lability.
URL: www.indiana.edu/~socpsy/ACT/math/eq_4.html
Document: David
Heise, "Affect Control Theory's Mathematical Model, With a List
of Testable Hypotheses. A Working Paper for ACT Researchers."
February 7, 1992. Revised and posted on the World Wide Web, April 15,
1997.
|
|
